ADT Tabulka
Vyhledávání v tabulkách

Klíčová slova

Cíle
Vytisknout studijní materiál

Zadání:

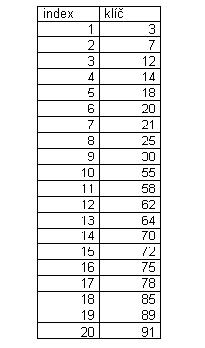
1, V zadané tabulce najděte metodou půlení intervalu (binární vyhledávání) klíč s hodnotou 85.

2, V té samé tabulce najděte klíč s hodnotou 85 pomocí Fibonacciho vyhledávání.

3, Vyberte si další prvek tabulky a rozhodněte které vyhledávání bude rychlejší. Určete obecné pravidlo.

Tipy pro řešení:

Na okraj tabulky si pište přístupy k prvku a číslujte 1...n. V jakém případě je lepší Fibonacciho princip?

šipka Návrh řešení:

1, Přístupy k jednotlivým klíčům jsou znázorněny v tabulce. Klíč 85 najdeme binárním vyhledáváním na 3 pokus.

2, Rozsah tabulky je 20. nejbližší Fibonacciho čéslo o 1 větší je 21. 21 rozdělím v poměru předchozích Fibonacciho čísel zmenšených o jednotku (7,12). Horní čast tabulky má délku 7, pak následuje prvek ke kterému přistoupím (8) a druhá část tabulky s délkou 12.

Klíč 25 < 85, proto hledám ve spodní části tabulky. Číslo 12 rozdělím (4, přístupový index, 7) atd. Viz tabulka:

3, Fibonacciho vyhledávání je rychlejší v tabulce ve které je většina prvků na začátku a naopak není výhodná pro tabulky s klíči na konci, nebo s klíči zakázanými.